Question

A pharmaceutical company claims that the average cold lasts an average of 8.4 days. They are using this as a basis to test new medicines designed to shorten the length of colds. A random sample of 106 people with colds, finds that on average their colds last 8.5 days. The population is normally distributed with a population standard deviation of 0.9 days. At α=0.02, what type of test is this and can you support the company’s claim using the p-value?

Answer 1

Answer with explanation:

Let
`\mu` be the population mean.

Null hypothesis :
`H_0:\mu=8.4`

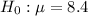
Alternative hypothesis :
`H_1:\mu<8.4`

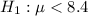
Since the alternative hypothesis is left tailed, so the test is a left-tailed test.

Sample size : n=106 >30 , so we use z-test.

Test statistic:
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`z=(8.5-8.4)/((0.9)/(√(106)))=1.14395890455\approx1.14`

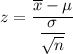
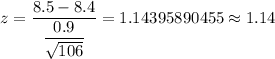
The P-value (Left tailed test)=
`P(z<1.14)= 0.8728568`

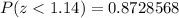
Since, the p-value is greater than the significance level , so we fail to reject the null hypothesis.

Hence, we cannot support the company's claim.