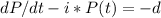Answer:
Deduction in the step-by-step explanation
Explanation:
If a P0=50.000 deposit is compound every instant, the ammount in the account can be modeled as:
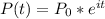
If you pull out d dollars a year, the equation becomes:
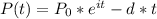
If we derive this equation in terms of t, we have
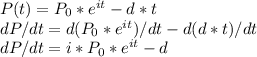
The first term can be transformed like this:

So replacing in the differential equation, we have
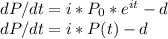
Rearranging