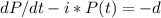Question

Your Aunt Matilda passes away and leaves you with the tidy sum of $50,000. You find a bank that will pay you 5.15 % per year compounded every instant. You want to enjoy some of this money, but you don't want to blow it away too fast. You decide to deposit the $50,000 but to pull out d dollars per year so that after t years, you will have blown (d t) dollars off. If P [t] is the amount in the account, then why does P [t] solve the differential equation P'[t] - 0.0515 P[t] = -d ?

Answer 1

Deduction in the step-by-step explanation

Explanation:

If a P0=50.000 deposit is compound every instant, the ammount in the account can be modeled as:

`P(t) = P_(0)*e^(it)`

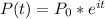
If you pull out d dollars a year, the equation becomes:

`P(t) = P_(0)*e^(it)-d*t`

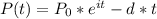
If we derive this equation in terms of t, we have

`P(t) = P_(0)*e^(it)-d*t\\dP/dt=d(P_(0)*e^(it))/dt-d(d*t)/dt\\dP/dt=i*P_(0)*e^(it)-d\\`

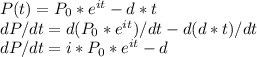
The first term can be transformed like this:

`i*P_(0)*e^(it) = i*P(t)`

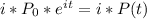
So replacing in the differential equation, we have

`dP/dt=i*P_(0)*e^(it)-d\\dP/dt=i*P(t)-d`

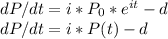
Rearranging

`dP/dt-i*P(t)=-d`