Question

The average fuel consumption for a Boeing 747 jet is normally distributed with a mean of 3245 gallons of jet fuel per hour and a standard deviation of 186 gallons per hour. (a) When a Boeing 747 is randomly selected what is the probability that its fuel consumption is between 3105 and 3498 jet fuel gallons per hour? (b) Rephrase your answer in (a) in the context of percentages (c) When a Boeing 747 is randomly selected what is the probability that its fuel consumption is more that 3498 jet fuel gallons per hour? (e) What is the fuel consumption per hour of the most efficient 10% of all Boeing 747 jets? (HINT: The Maryland car example in your notes references ""miles per gallon"". Higher miles per gallon means that the car is more efficient. But this example references ""gallons per hour"". Less gallons per hour means that the jet is more efficient).

Answer 1

(a) 0.13894 (b) 13,89% (c) 0.08688 (e) 3006 gal/hr or less

Explanation:

(a) The fuel consumption is normally distributed N(μ=3245,σ=186).

The z-scores for 3105 and 3498 are

`z=((X-\mu))/(\sigma )\\\\z1=(3105-3245)/186 = 0.7527\\z2=(3498-3245)/186 = 1.3602\\`

We can calculate the probability of fuel consumption bieng between 3105 and 3498 as:

P(0.7527<z<1.3602) = P(z<1.3602) - P(z<0.7527)

The probability of the fuel consumption being smaller than 3498 is

P(z<1.3602) = 0.91312

and the probability of the fuel consumption being smaller than 3105 is

P(z<0.7527) = 0.77418

Then

P(0.7527<z<1.3602) = P(z<1.3602) - P(z<0.7527)

P(0.7527<z<1.3602) = 0.91312-0.77418 = 0.13894 or 13.89%

(c) For a fuel consumption of 3498, we calculate z=1.3602

P(fuel consumption>3498) = P(z>1.3602)=1-P(z<1.3602)

P(fuel consumption>3498) = 1-0.91312 = 0.08688

(e) The 10% most efficient planes satisfy the next equation:

P(fuel consumption<X) = P(z<z1) = 0,1

Looking at the probabilities table, z1=-1.28155

Knowing z1, we can calculate X as

`z=((X-\mu))/(\sigma )\\\\X=\mu+\sigma*z\\X=3245+186*(-1.28155)= 3006`

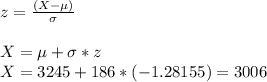
The fuel consumption of the 10% most efficient Boeing 747 jets is 3006 gallons per hour or less