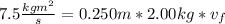Answer:

Step-by-step explanation:
We can solve this problem using conservation of angular momentum.
The angular momentum
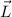 is
is
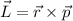
where
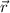 is the position and
is the position and
 the linear momentum.
the linear momentum.
We also know that the torque is
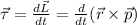
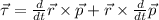
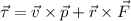
but, as the linear momentum is
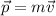 this means that is parallel to the velocity, and the first term must equal zero
this means that is parallel to the velocity, and the first term must equal zero

so
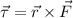
But, as the only horizontal force is the tension of the string, the force must be parallel to the vector position measured from the vertical rod, so
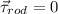
this means, for the angular momentum measure from the rod:
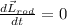
that means :
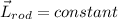
So, the magnitude of initial angular momentum is :
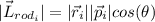
but the angle is 90°, so:
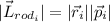
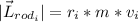
We know that the distance to the rod is 0.750 m, the mass 2.00 kg and the speed 5 m/s, so:
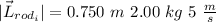
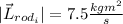
For our final angular momentum we have:
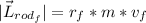
and the radius is 0.250 m and the mass is 2.00 kg
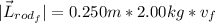
but, as the angular momentum is constant, this must be equal to the initial angular momentum