Answer:
The minimum coefficient of static friction is: 0.5
Step-by-step explanation:
We need to represent the forces of the display board (see attached) as free body diagram. Then we need to remember that the display board is in translational and rotational equilibrium, so we can sum of forces acting to x axis and y axis getting from the sum of forces acting at x axis as:
 , we need to remember that friction force is:
, we need to remember that friction force is:
 where u is the friction coefficient and N is the normal force at the surfaces in contact so replacing we get:
where u is the friction coefficient and N is the normal force at the surfaces in contact so replacing we get:
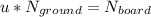 , so
, so
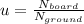 this is the equation (1). Now we need to sum forces at y axis:
this is the equation (1). Now we need to sum forces at y axis:
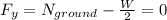 , so
, so
 . For doing the rotational equilibrium, we need to choose the ground as the point about which to take the torques:
. For doing the rotational equilibrium, we need to choose the ground as the point about which to take the torques:
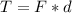 , this is for convenience because two forces passes through the point, as a result they don't have moment arm so we get:
, this is for convenience because two forces passes through the point, as a result they don't have moment arm so we get:
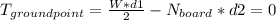 , so
, so
 , this is the equation (2). Assuming that the board has a height as: L and remember that was cutting it in half, both sides have as longitude:L/2 and applying trigonometric identities, we can find as:
, this is the equation (2). Assuming that the board has a height as: L and remember that was cutting it in half, both sides have as longitude:L/2 and applying trigonometric identities, we can find as:
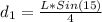 and
and
 (see attached), and replacing this at equation (2), we get:
(see attached), and replacing this at equation (2), we get:
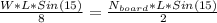 and solving to Nboard we get
and solving to Nboard we get
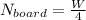 . Now we can replace those results at equation (1), Now we can find the friction coefficient as:
. Now we can replace those results at equation (1), Now we can find the friction coefficient as:
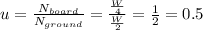 .
.