Question

Which of the following equations represents a line that is parallel to the line represented by 3x + 5y = –3? A. 3x + 5y = 2 B. 6x + 10y = –6 C. –5x + 3y = 2 D. –3x + 5y = –3

Answer 1

Option b

The equation 6x + 10y = -6 represents a line that is parallel to the line 3x + 5y = –3

Solution:

let us consider two equations

`a_(1) x_(1) + b_(1) y_(1) + c_(1) = 0`

`a_(2) x_(2) + b_(2) y_(2) + c_(2) = 0`

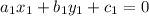
If two equations are parallel to each other,then the condition is

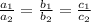`(a_(1))/(a_(2)) = (b_(1))/(b_(2)) = (c_(1))/(c_(2))` ------------- eqn 1

From question, given that 3x + 5y = –3

Hence we get,
`a_(1) = 3, b_(1) = 5 \text { and } c_(1) = -3`

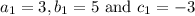
Applying equation 1 in the given options,

Case 1:

Consider option 1, given that 3x + 5y = 2

Hence we get,
`a_(2) = 3, b_(2) = 5 \text { and } c_(2) = 2`

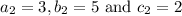
By using equation 1,

`(3)/(3) = (5)/(5) \\eq (-3)/(2)`

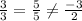
Hence the condition is not satisfied.

Case 2:

Consider option 2, given that 6x + 10y = –6

Hence we get,
`a_(2) = 6 \text { and } b_(2) = 10 \text { and } c_(2) = -6`

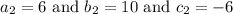
By using equation 1,

`(3)/(6) = (5)/(10) = (-3)/(-6)`

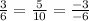
By simplifying we get,

`(1)/(2) = (1)/(2) = (1)/(2)`

Hence the condition is satisfied. So, 6x + 10y = –6 represents the line which is parallel to 3x + 5y = –3

Case 3:

Consider option 3, given that -5x + 3y = –2

Hence we get,
`a_(2) = -5 \text { and } b_(2) = 3 \text { and } c_(2) = -2`

By using equation 1,

`(3)/(-5) \\eq (5)/(3) \\eq (-3)/(-2)`

Hence the condition is not satisfied.

Case 4:

Consider option 4, given that –3x + 5y = –3

Hence we get
`a_(2) = -3 \text { and } b_(2 )= 5 \text { and } c_(2) = -3`

By using equation 1,

`(3)/(-3) \\eq (5)/(5) \\eq (-3)/(-3)`

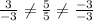
Hence the condition is not satisfied.

Thus the correct answer is option b