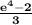The value of x in ln(3x + 2) = 4 is
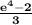
Answer:
Option a
Solution:
From question, given that ln(3x + 2) = 4
ln(3x + 2) = 4 ----- eqn 1
By raising “e” to the power of both sides of equation, the above equation becomes
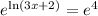
“ln” and “e” cancel out each other in left hand side of above equation. Hence we get
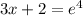
Rearranging the terms, the above equation becomes,
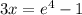
x =
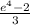
Thus the value of x in ln(3x + 2) = 4 is