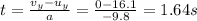Question

1.) A ski jump is angled at 40° and the skier is launched at 25 m/s. A.) What was her highest

point above the end of the ramp? B.)How much time does it take her to reach the highest point?

Answer 1

A) 13.2 m

The motion of the skier is a projectile motion, which consists of two independent motions:

- a horizontal motion with constant speed

- a vertical motion with constant acceleration
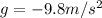`g=-9.8 m/s^2` (acceleration of gravity) downward

To find the maximum height of her trajectory, we are only concerned with her vertical motion.

The initial vertical velocity upward is

`u_y = u_0 sin \theta = (25) sin 40^(\circ) =16.1 m/s`

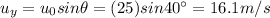
then we can use the following SUVAT equation:

`v_y^2 - u_y^2 = 2ah`

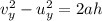
where

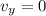`v_y=0` is the final vertical velocity, which is zero at the maximum height

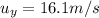`u_y = 16.1 m/s` is the initial vertical velocity

`a=g=-9.8 m/s^2`

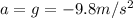
h is the maximum height

Solving for h,

`h=(v_y^2-u_y^2)/(2g)=(-(16.1)^2)/(2(-9.8))=13.2 m`

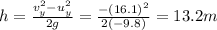
B) 1.64 s

The time needed to reach the highest point can be found by analyzing again the vertical motion only. In fact, we can use the following SUVAT equation:

`v_y = u_y +at`

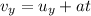
where

`u_y = 16.1 m/s`

`a=g=-9.8 m/s^2`

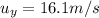
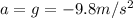
At the maximum height, the vertical velocity is zero:

`v_y=0`

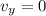
So we can solve the equation to find the corresponding time:

`t=(v_y-u_y)/(a)=(0-16.1)/(-9.8)=1.64 s`