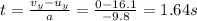A) 13.2 m
The motion of the skier is a projectile motion, which consists of two independent motions:
- a horizontal motion with constant speed
- a vertical motion with constant acceleration
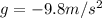 (acceleration of gravity) downward
(acceleration of gravity) downward
To find the maximum height of her trajectory, we are only concerned with her vertical motion.
The initial vertical velocity upward is
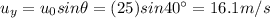
then we can use the following SUVAT equation:
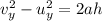
where
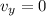 is the final vertical velocity, which is zero at the maximum height
is the final vertical velocity, which is zero at the maximum height
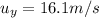 is the initial vertical velocity
is the initial vertical velocity
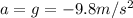
h is the maximum height
Solving for h,
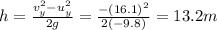
B) 1.64 s
The time needed to reach the highest point can be found by analyzing again the vertical motion only. In fact, we can use the following SUVAT equation:
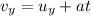
where
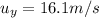
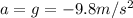
At the maximum height, the vertical velocity is zero:
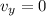
So we can solve the equation to find the corresponding time: