Let
 be the two roots. The claim is that
be the two roots. The claim is that

We can rewrite this expression as
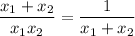
Now, recall that if the leading term is 1, then you can think of a quadratic equation as
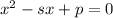
i.e. the linear coefficient is the opposite of the sum of the roots, and the constant term is the product of the roots. In other words, we have
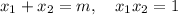
Substitute these values in the equation above to have

Which leads to
