Step-by-step explanation:
The given data is as follows.
Diameter = 0.1 m,
 = 1000 kPa
= 1000 kPa
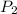 = 500 kPa
= 500 kPa
Change in pressure
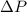 = 1000 kPa - 500 kPa = 500 kPa
= 1000 kPa - 500 kPa = 500 kPa
Since, 1000 Pa = 1 kPa. So, 500 kPa will be equal to
 .
.
Q = 5
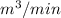 =
=
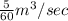 = 0.0833
= 0.0833
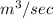
It is known that Q =

where, A = cross sectional area
V = speed of the fluid in that section
Hence, calculate V as follows.
V =
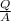
=
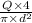
=
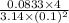
= 10.61 m/sec
Also it is known that Reynold's number is as follows.
Re =
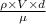
=
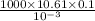
= 1061032.954
As, it is given that the flow is turbulent so we cannot use the Hagen-Poiseuille equation as follows. Therefore, by using Blasius equation for turbulent flow as follows.
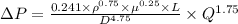
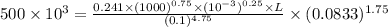
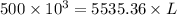
L =
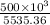
= 90.328 m
Thus, we can conclude that 90.328 m length galvanized iron line should be used to reach the desired outlet pressure.