Question

You are requested to reduce the size of 50 ton/hr of a given solid. The size of the feed is such 80% passes a 4-in (76.2 mm) screen and 80 % of the product passes a (1/4) inch ( 3.175 mm). Knowing the work index of the solid (Ei=9.45), calculate the required power for the operation in hp. ACTIVITY II A packed bed is composed of spheres having a diameter of 12 mm. The bulk density of the overall packed bed is 990 kg/m3 and the density of solid spheres is 1570 kg/m3. Calculate the void fraction of the bed.

Answer 1

1) The power needed to process 50 ton/hr is 135.4 HP.

2) The void fraction of the bed is 0.37.

Step-by-step explanation:

1) For this type of milling operations, we can estimate the power needed for an operation according to the work index (Ei), the passing size of the circuit feed (F80) and the passing size of the product (P80).

We assume the units of Ei are kWh/t.

The equation that relates this parameters and the power is (size of particles in μm):

`W=Ei*((10)/(√(P80)) -(10)/(√(F80)) )\\\\W=9.45*((10)/(√(3175\mu m)) -(10)/(√(76200mm)) )\\\\\\W=9.45*(0.1774+0.0362)=2.019 kWh/t`

The power needed to process 50 ton/hor is

`P=2.0194(kWh)/(Ton)*(50Ton)/(h)*(1.341HP)/(1kW)=   135.4 \, HP`

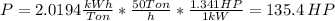
2) The density of the packed bed can be expressed as

`\rho=f_v*\rho_v+f_s*\rho_s`

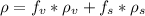
being f the fraction and ρ the density of every fraction. We know that the density of the void is 0 (ρv=0) and that fv=1-fs (the sum of the fractions ois equal to the total space).

Then we can rearrange

`\rho=f_v*\rho_v+f_s*\rho_s\\\\\rho=f_v*0+(1-f_v)*\rho_s\\\\\rho/\rho_s=1-f_v\\\\f_v=1-\rho/\rho_s=1-990/1570=1-0.63=0.37`

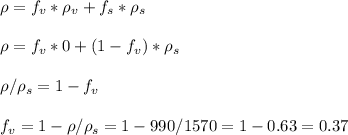
The void fraction of the bed is 0.37.