Answer:
The system consists of parallel lines ⇒ 2nd answer
Both lines have the same slope ⇒ 3rd answer
Explanation:
Lets revise the types of the solutions of the system of equations
Case 1:
→ If the two equations have the same coefficients of the two variables
and different numerical terms then the two equations represented
by two parallel lines
Ex: ax + by = c , ax + by = d
Case 2:
→ If the two equations have the same coefficients of the two variables
and same numerical term then the two equations represented
by the same line
Ex: ax + by = c , ax + by = c
Case 3:
→ If the two equations have different coefficients of one of the variables
or the two variables then they represented by two intersected lines
and the system has one solution
Ex: ax + by = c , dx + ey = f
The system of equation is
* y =
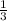 x - 4
x - 4
* 3 y - x = -7
Multiply the first equation by 3
∴ 3 y = x - 12
Subtract both sides by x
∴ 3 y - x = - 12 ⇒ (1)
∵ 3 y - x = - 7 ⇒ (2)
The system of equations has same x-coefficient and same y-coefficient
in both equations but the numerical terms are different, then they
represented by two parallel lines as first case above
and parallel lines have the same slope
The system consists of parallel lines
Both lines have the same slope