Question

One mole of pure N2 and 1 mole of pure O2 are contained in separate compartments of a rigid and insulated container at 1 bar and 298 K. The separator between the compartments are later removed to allow the mixing of the gases. Assume that both gases are in the ideal gas state.

a) What is the final T and P of the mixture?

b) For a mixture of ideal gases, each component carries a partial pressure that is proportional to its mole fraction: i.e., p????2 = y????2 P and p????2 = y????2 P, P being the total pressure of the mixture. Calculate the entropy change of the mixing process and draw a schematic showing the hypothetical path you used for the calculation.

I am unclear why you need enthalpy information when the question asks for entropy. Can someone please solve part A?

Answer 1

a. T and P remain the same (T=298 K and P=1 bar)

b. 11.23J/K

Step-by-step explanation:

a. Since the mixing process of an idea gas doesn't present a change in the enthalpy, we could state that no change in neither temperature and pressure are given.

b. It is not necessary to know enthalpy data, the following formula is enough to compute the entropy change:

Δ
`S_(mix)=-n_(N_2)R ln(x_(N_2))-n_(O_2)R ln(x_(O_2))`

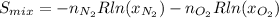
Thus, the molar fractions are equal to 0.5, and the result yields:

Δ
`S_(mix)=-(1mol)[(8.314J/(mol*K)]ln(0.5)-(1mol)[(8.314J/(mol*K)]ln(0.5)`

Δ
`S_(mix)=11.23J/K`

Best regards