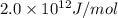Question

What is the nuclear binding energy of He? Mass of He nucleus 4.00150 amu Mass of a proton 1.00728 amu 1.00866 amu Mass of a neutron 2.9979*10 m/s Speed of light 6.022x103 Abogadro's number

Answer 1

Answer : The nuclear binding energy of He for one mole is
`2.0* 10^(12)J/mol`

Explanation :

The isotopic representation of He :
`_(2)^(4)\textrm{He}`

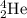
Atomic number = Number of protons = 2

Mass number = 4

Number of neutrons = Mass number - Atomic number = 4 - 2 = 2

To calculate the mass defect of the nucleus, we use the equation:

`\Delta m=[(n_p* m_p)+(n_n* m_n)+]-M`

where,

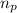`n_p` = number of protons = 2

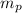`m_p` = mass of one proton = 1.00728 amu

`n_n` = number of neutrons = 2

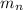`m_n` = mass of one neutron = 1.00866 amu

M = Nuclear mass number = 4.00150 amu

Putting values in above equation, we get:

`\Delta m=[(2* 1.00728)+(2* 1.00866)]-[4.00150]\\\\\Delta m=0.03038amu`

Now converting the value of amu into kilograms, we use the conversion factor:

`1amu=1.66* 10^(-27)kg`

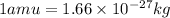
So,
`0.03038amu=0.03038* 1.66* 10^(-27)kg=0.0504* 10^(-27)kg`

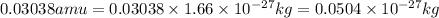
To calculate the equivalent energy, we use the equation:

`E=\Delta mc^2`

E = nuclear binding energy = ?

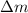`\Delta m` = mass change =
`0.0504* 10^(-27)kg`

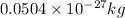
c = speed of light =
`3* 10^8m/s`

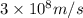
Putting values in above equation, we get:

`E=(0.0504* 10^(-27)kg)* (3.0* 10^8m/s)^2\\\\E=4* 10^(-12)J`

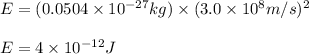
Nuclear binding energy for one mole is:

`E=(4.0* 10^(-12)J)* (6.022* 10^(23)mol^(-1))=2.0* 10^(12)J/mol`

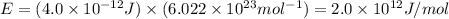
Therefore, the nuclear binding energy of He for one mole is
`2.0* 10^(12)J/mol`