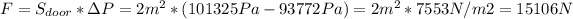Question

An air tight freezer measures 4 mx 5 m x 2.5 m high. With the door open, it fills with 22 °C air at 1 atm pressure.

a. Calculate the density of this air in kg/m3

b. After closing the door it is cooled down to 7 °C. How low will the pressure in the freezer

be in units of Pa and mmHg?

C. How many newtons of force will be needed to open the 1 m x 2 m door?

Answer 1

(a) Density of the air = 1.204 kg/m3

(b) Pressure = 93772 Pa or 0.703 mmHg

(c) Force needed to open the door = 15106 N

Step-by-step explanation:

(a) The density of the air at 22 deg C and 1 atm can be calculated using the Ideal Gas Law:

`\rho_(air)=(P)/(R*T)`

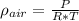
First, we change the units of P to Pa and T to deg K:

`P=1 atm * (101,325Pa)/(1atm)=101,325 Pa\\\\ T=22+273.15=293.15^(\circ)K`

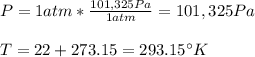
Then we have

`\rho_(air)=(P)/(R*T)=(101325Pa)/(287.05 J/(kg*K)*293.15K) =1.204 (kg)/(m3)`

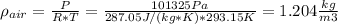
(b) To calculate the change in pressure, we use again the Ideal Gas law, expressed in another way:

`PV=nRT\\P/T=nR/V=constant\Rightarrow P_(1)/T_(1)=P_(2)/T_(2)\\\\P_(2)=P_(1)*(T_(2))/(T_(1))=101325Pa*(7+273.15)/(22+273.15)=101,325Pa*0.9254=93,772Pa\\\\P2=93,772 Pa*(1mmHg)/(133,322Pa)= 0.703 mmHg`

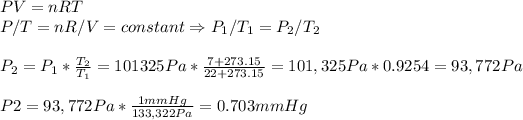
(c) To calculate the force needed to open we have to multiply the difference of pressure between the inside of the freezer and the outside and the surface of the door. We also take into account that Pa = N/m2.

`F=S_(door)*\Delta P=2m^(2) *(101325Pa - 93772Pa)=2m^(2) *7553N/m2=15106N`