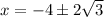Question

What are the zeros of the function f(x)=x^2+8x+4, expressed in the simplest radical form ?

Answer 1

`x=-4 \pm 2√(3)`

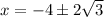
Explanation:

The zeros of f is when f=0.

So we need to solve:

`x^2+8x+4=0`

-----------------------------------------------------------------------------------------------------

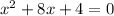
I'm going to choose completing the square.

Subtract 4 on both sides:

`x^2+8x=-4`

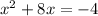
Add (8/2)^2 on both sides:

`x^2+8x+((8)/(2))^2=-4+((8)/(2))^2`

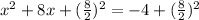
Write left hand side as a square:

`(x+(8)/(2))^2=-4+4^2`

`(x+4)^2=-4+16`

`(x+4)^2=12`

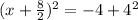
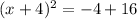
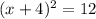
Take the square root of both sides:

`(x+4)=\pm √(12)`

`x+4=\pm √(12)`

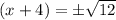
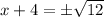
Simplify right hand side:

`x+4=\pm √(4)√(3)`

`x+4=\pm 2√(3)`

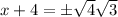
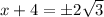
Subtract 4 on both sides:

`x=-4 \pm 2√(3)`

---------------------------------------------------------------------------------------------

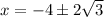
You could also go with quadratic formula:

`a=1`

`b=8`

`c=4`

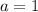
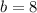
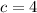
We need to use this formula:

`x=(-b\pm √(b^2-4ac))/(2a)`.

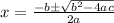I'm going to evaluate
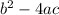`b^2-4ac` first.

`b^2-4ac=(8)^2-4(1)(4)=64-16=48`

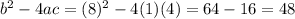
So now we have this so for with the formula:

`x=(-8 \pm √(48))/(2(1))`

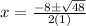
Simplifying the denominator gives:

`x=(-8 \pm √(48))/(2)`

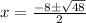
Now is there a perfect square in 48? Yes, 16 is a perfect square factor in 48.

So we can write:

`x=(-8 \pm √(16)√(3))/(2)`

`x=(-8 \pm 4√(3))/(2)`

`x=(-8)/(2)\pm (4√(3))/(2)`

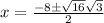
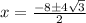
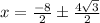
Reduce fractions:

`x=-4 \pm 2√(3)`