Question

Use mathematical induction to prove that for each integer n ≥ 4, 5^n ≥ 2 2^n+1 + 100

Answer 1

The given Statement which we have to prove using mathematical induction is

`5^n\geq 2*2^(n+1)+100`

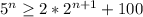
for , n≥4.

⇒For, n=4

LHS

`=5^4\\\\5*5*5*5\\\\=625\\\\\text{RHS}=2.2^(4+1)+100\\\\=64+100\\\\=164`

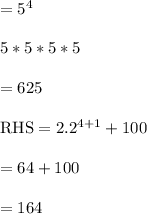
LHS >RHS

Hence this statement is true for, n=4.

⇒Suppose this statement is true for, n=k.

`5^k\geq 2*2^(k+1)+100`

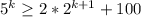
-------------------------------------------(1)

Now, we will prove that , this statement is true for, n=k+1.

`5^(k+1)\geq 2*2^(k+1+1)+100\\\\5^(k+1)\geq 2^(k+3)+100`

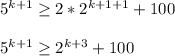
LHS

`5^(k+1)=5^k*5\\\\5^k*5\geq 5 *(2*2^(k+1)+100)----\text{Using 1}\\\\5^k*5\geq (3+2) *(2*2^(k+1)+100)\\\\ 5^k*5\geq 3* (2^(k+2)+100)+2 *(2*2^(k+1)+100)\\\\5^k*5\geq 3*(2^(k+2)+100)+(2^(k+3)+200)\\\\5^(k+1)\geq (2^(k+3)+100)+3*2^(k+2)+400\\\\5^(k+1)\geq (2^(k+3)+100)+\text{Any number}\\\\5^(k+1)\geq (2^(k+3)+100)`

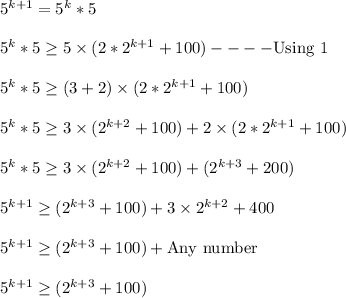
Hence this Statement is true for , n=k+1, whenever it is true for, n=k.

Hence Proved.