The given Statement which we have to prove using mathematical induction is
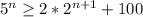
for , n≥4.
⇒For, n=4
LHS

LHS >RHS
Hence this statement is true for, n=4.
⇒Suppose this statement is true for, n=k.

-------------------------------------------(1)
Now, we will prove that , this statement is true for, n=k+1.
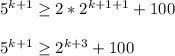
LHS
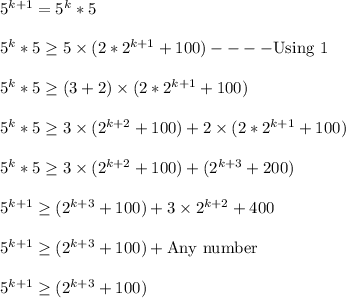
Hence this Statement is true for , n=k+1, whenever it is true for, n=k.
Hence Proved.