Question

You notice that the water in your friend's swimming pool is cloudy and that the pool walls are discolored at the water line. A quick analysis reveals that the pH of the water is 8.40 when it should be 7.20. The pool is 7.00 m wide, 18.0 m long, and has an average depth of 1.50m What is the minimum (in the absence of any buffering capacity) volume (mL) of 12.0 wt% H2SO4 (SG 1.080) that should be added to return the pool to the desired pH? mL

Answer 1

3,78 mL of 12,0wt% H₂SO₄

Step-by-step explanation:

The equilibrium in water is:

H₂O (l) ⇄ H⁺ (aq) + OH⁻ (aq)

The initial concentration of [H⁺] is 10⁻⁸ M and final desired concentration is [H⁺] =
`10^(-7,2)`

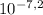
Thus, you need to add:

[H⁺] =
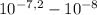`10^(-7,2) - 10^(-8)` = 5,31x10⁻⁸ M

The total volume of the pool is:

7,00 m × 18,0 m ×1,50 m = 189 m³ ≡ 189000 L

Thus, moles of H⁺ you need to add are:

5,31x10⁻⁸ M × 189000 L = 1,00x10⁻² moles of H⁺

These moles comes from

H₂SO₄ → 2H⁺ +SO₄²⁻

Thus:

1,00x10⁻² moles of H⁺ ×
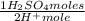`(1 H_(2)SO_(4) moles)/(2H^+ mole)` = 5,00x10⁻³ moles of H₂SO₄

These moles comes from:

5,00x10⁻³ moles of H₂SO₄ ×
`(98,1g)/(1mol)` ×
`(100 gsolution)/(12 g H_(2)SO_(4) )` ×
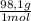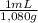`(1mL)/(1,080 g)` = 3,78 mL of 12,0wt% H₂SO₄

I hope it helps!