Step-by-step explanation:
Relation between length of a curve and angle is as follows.
l =

where, R = radius of curve
 = angle in radians
= angle in radians
Also, l =
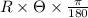 .......... (1)
.......... (1)
If curve has a degree of curvature
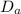 for standard length s, then
for standard length s, then
R =
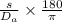 ........... (2)
........... (2)
Now, substitute the value of R from equation (2) into equation (1) as follows.
l =

If s = 30 m, then calculate the value of l as follows.
l =

=
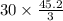
= 452 m
thus, we can conclude that the length of the curve is 452 m.