Question

Find the area of the triangle defined by the coordinates (7,1), (0,10), and (9,4). (To the nearest tenth).

Answer 1

`\boxed{Area=19.5units^2}`

Explanation:

A triangle is any polygon with exactly 3 sides. Let's call this sides the vertices of the triangle, and let's say:

`(7,1)=A(7,1) \\ \\ (0,10)=B(0,10) \\ \\ (9,4)=C(9,4)`

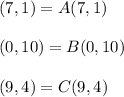
Where:

`A=(A_(x),A_(y)) \\ B=(B_(x),B_(y)) \\ C=(C_(x),C_(y))`

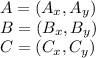
A formula for finding the area of a triangle given its vertices is:

`Area=|(A_(x)(B_(y)-C_(y))+B_(x)(C_(y)-A_(y))+C_(x)(A_(y)-B_(y)))/(2)| \\ \\ Area=|(7(10-4)+0(4-1)+9(1-10))/(2)| \\ \\ Area=|(-39)/(2)| \\ \\ \boxed{Area=19.5units^2}`

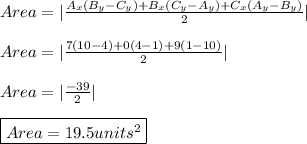
Finally, the area of the triangle defined by the coordinates (7,1), (0,10), and (9,4), to the nearest tenth is 19.5 squared units.