Answer:

Explanation:
A triangle is any polygon with exactly 3 sides. Let's call this sides the vertices of the triangle, and let's say:
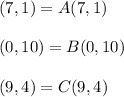
Where:
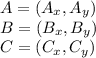
A formula for finding the area of a triangle given its vertices is:

Finally, the area of the triangle defined by the coordinates (7,1), (0,10), and (9,4), to the nearest tenth is 19.5 squared units.