Question

The tallest sequoia sempervirens tree in California’s redwood national parks is 111 m tall. Suppose an object is thrown downward from the top of that tree with a certain initial velocity. If the object reaches the ground in 3.80 s, what is the objects initial velocity?

Answer 1

The object's initial velocity is equal to
`-10.59(m)/(s)`

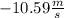
Why?

From the statement we know the height of the tree and the time it takes to reach the ground, so, if we need to calculate its initial velocity, we can use the following formula:

`y=y_o-v_(o)*t-(1)/(2)g*t^(2)`

Where,

y, is the final height (0 meters in this case)

yo, is the initial height (111 meters in this case)

t, is the time elapsed (3.8 seconds in this case)

vo, is the initial speed.

g, is the acceleration due to gravity (-9.81 m/s2)

Now, let's set the origin at the top of the tree, so, rewriting the formula, we have:

`y=y_o+v_(o)*t+(1)/(2)g*t^(2)`

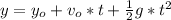
So, isolating the initial velocity, we have:

`y=y_o+v_(o)*t+(1)/(2)g*t^(2)`

`y=y_o+v_(o)*t+(1)/(2)g*t^(2)\\\\v_(o)*t=y-y_o-(1)/(2)g*t^(2)\\\\v_(o)=(y-y_o-(1)/(2)g*t^(2))/(t)`

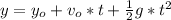
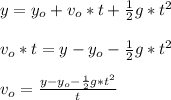
Finally, substituting and calculating, we have:

`v_(o)=(-111m-0-(1)/(2)(-9.8(m)/(s^(2))) *(3.8s)^(2)))/(3.8s)\\\\v_(o)=(-111m-(1)/(2)(-9.8(m)/(s^(2)))*(14.44s^(2)))/(3.8s)\\\\v_(o)=(-111m-(1)/(2)(-141.51m))/(3.8s)=(-111m+70.75m)/(3.8s)\\\\v_(o)=(-40.25m)/(3.8s)=-10.59(m)/(s)`

Hence, we have that the initial velocity of the object is
`-10.59(m)/(s)`

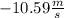
Have a nice day!