Question

A population of bacteria is growing exponentially. At 7:00 a.m. the mass of the population is 12 mg. Five hours later it is 14 mg. (a) What will be the mass of the bacteria after another 5 hours? (b) At 7:00 p.m. what do we expect the mass to be? (c) What was the mass of the population at 8:00 a.m.? Given your answer, by what percent is the mass of the population increasing each hour? By what percent is it increasing each day?

Answer 1

Answer with Step-by-step explanation:

The exponential growth function is given by

`N(t)=N_oe^(mt)`

where

`N(t)` is the population of the bacteria at any time 't'

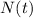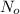`N_o` is the population of the bacteria at any time 't = 0'

'm' is a constant and 't' is time after 7.00 a.m in hours

Assuming we start our measurement at 7.00 a.m as reference time t = 0

Thus we get
`N(0)=N_oe^(m* 0)\\\\12=N_o`

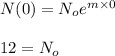
Now since it is given after 5 hours the population becomes 14 mg thus from the above relation we get

`12* e^(m* 5)=14\\\\e^(5m)=(14)/(12)\\\\m=(1)/(5)\cdot ln((14)/(12))\\\\m=0.031`

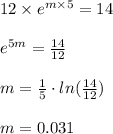
Thus the population of bacteria at any time 't' is given by

`N(t)=12e^(0.031t)`

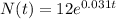
Part a)

Population of bacteria after another 5 hours equals the population after 10 hours from start

`N(10)=12e^(0.031* 10)=16.361mg`

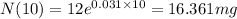
Part b)

Population of bacteria at 7:00 p.m is mass after 12 hours

`N(1)=12e^(0.031* 12)=17.41mg`

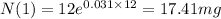
Part c)

Population of bacteria at 8:00 p.m is mass after 1 hour

`N(1)=12e^(0.031* 1)=12.3378mg`

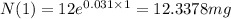
Part d)

Differentiating the relation of population with respect to time we get

`N'(t)=(d(12\cdot e^(0.031t)))/(dt)\\\\N'(t)=12* 0.031=0.372e^(0.031t)`

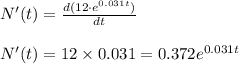
Thus we can see that the percentage increase varies with time initially the percentage increase is 37.2% but this percentage increase increases with increase in time

Part 4)

Since there are 24 hours in 1 day thus the percentage increase in the population is

`(N(24)-N_o)/(N_o)* 100\\\\=(25.25-12)/(12)* 100=110.42`

Thus there is an increase of 110.42% in the population each day.