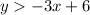Answer:
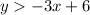
Explanation:
First find the equation of the "boundary line" that separates the two sections of the plane. It is very simple to find its slope_y-intercept form from the graph.
We can find the slope of the boundary line by examining the two points where it intersects the axes: It crosses the y-axis at (0,6) (0 for x, 6 units for y)
and also crosses the x axis at (2,0) (2 unites for x and 0 for y)
That means that from the y intersect crossing, in order to arrive at the x intersect crossing, one has to go:
2 units to the right (this is called "run")
and 6 units down (this is called "rise", but should be considered as a negative value because instead of "rising" is going down)
Therefore, the slope of the boundary line is:
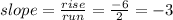
We also see that the y-intercept is = 6 (the point at which the line crosses the y-axis.
Then, we can write the equation of the boundary line as:
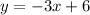
Now, the set of (x,y) points that are highlighted in the picture are those "ABOVE" the boundary line, that is those points where the y-value is greater than those defined by the boundary line. Since the boundary line is drawn with a dotted line, that indicates that those values corresponding to (x,y) values in the line itself should NOT be included.
We therefore arrive at an inequality that does not contain an equal sign (to preclude the actual (x,y) values in the line to be included). and which indicates that we want all the (x,y) points on the plane which have y-values greater than those define by the boundary line. That is: