Answer: The correct options are
(1) (D) 0.30
(2) (A) 20%
(3) (C) 24.5%.
Step-by-step explanation: We are given to answer all the following three questions.
(1) Given that A and B are independent events, where
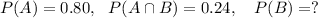
We know that
if S and T are independent events, then
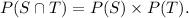
Therefore, we get
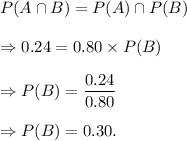
Option (D) is CORRECT.
(2) Given that a weather forecaster predicts that their is 50% chance of rain on Saturday and a 40% chance of rain on Sunday.
We are to find the probability that it will rain both days.
Let X and Y represents the probabilities that it will rain on Saturday and Sunday respectively.
Then, we have
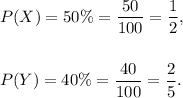
Since X and Y are independent of each other, so the probability that it will rain both days is

Option (A) is CORRECT.
(3) Given that a card is randomly drawn from a shuffled deck of cards and NOT REPLACED. A second card is drawn from the remaining shuffled cards.
We are to find the probability that both cards are RED.
Since there are 26 red cards in a pack of 52 cards, so the probability of drawing first red card is
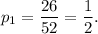
Without replacement, the probability of drawing second red card will be
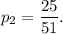
Therefore, the probability that both cards are red is
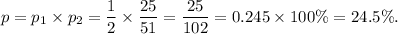
Option (C) is CORRECT.
Thus, (D), (A) and (C) are correct options.