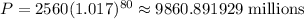Question

Use the fact that the world population was 2560 million in 1950 and 3040 million in 1960 to model the population of the world in the second half of the 20th century. (Assume that the growth rate is proportional to the population size.) What is the relative growth rate? Use the model to estimate the world population in 1992 and to predict the population in the year 2030. SOLUTION We measure the time t in years and let t = 0 in the year 1950. We measure the population P(t) in millions of people. Then P(0) = 2560 and P(10) = 3040. Since we are assuming that dP/dt = kP, this theorem gives the following. (Round to six decimal places.)

Answer 1

Let the growth function that shows the population in millions after x years,

`P=P_0(1+r)^x`

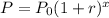
Where,

`P_0` = initial population,

r = growth rate per year,

Suppose the population is estimated since 1950,

Thus, if x = 0, P = 2560,

`\implies 2560 = P_0 (1+r)^0\implies P_0 = 2560`

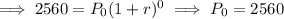
Now, if x = 10 ( that is, on 1960 ), P = 3040,

`3040=2560(1+r)^(10)\implies r = 0.017`

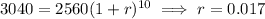
Hence, the required function that shows the population after x years,

`P=2560(1.017)^x`

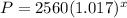
If x = 42,

The population in 1992 would be,

`P=2560(1.017)^(42)\approx 5196.608365\text{ millions}`

if x = 80,

The population in 2030 would be,

`P=2560(1.017)^(80)\approx 9860.891929\text{ millions}`