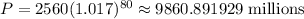Answer:
Let the growth function that shows the population in millions after x years,
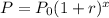
Where,
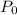 = initial population,
= initial population,
r = growth rate per year,
Suppose the population is estimated since 1950,
Thus, if x = 0, P = 2560,
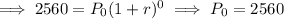
Now, if x = 10 ( that is, on 1960 ), P = 3040,
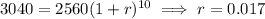
Hence, the required function that shows the population after x years,
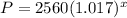
If x = 42,
The population in 1992 would be,
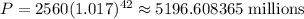
if x = 80,
The population in 2030 would be,