Question

What is the length of BC in the right triangle below?

Answer 1

E:75

Explanation:

`\sqrt{21^(2) +72^(2)}`

Answer 2

Answer : The length of BC in the right triangle is, 75

Step-by-step explanation :

Using Pythagoras theorem in ΔBAC :

`(Hypotenuse)^2=(Perpendicular)^2+(Base)^2`

`(BC)^2=(AB)^2+(AC)^2`

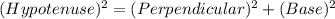
Given:

Side AB = 21

Side AC = 72

Now put all the values in the above expression, we get the value of side BC.

`(BC)^2=(21)^2+(72)^2`

`BC=√((21)^2+(72)^2)`

`BC=√(441+5184)`

`BC=√(5625)`

`BC=75`

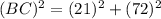
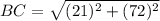
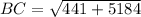
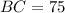
Therefore, the length of BC in the right triangle is, 75