Answer : The length of BC in the right triangle is, 75
Step-by-step explanation :
Using Pythagoras theorem in ΔBAC :
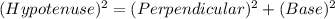
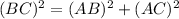
Given:
Side AB = 21
Side AC = 72
Now put all the values in the above expression, we get the value of side BC.
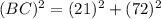
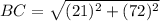
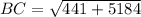
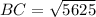
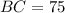
Therefore, the length of BC in the right triangle is, 75