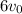Answer:
Step-by-step explanation:
The speed of the particle increases linearly with time, so we can write it as
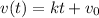
where k is the a certain constant of proportionality and
 is the initial speed.
is the initial speed.
We also know that at t = 4 s, the speed is
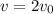 , so we can use this information to find k:
, so we can use this information to find k:

So the complete expression of v(t) is
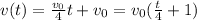
Now we integrate the quantity
 , and we find:
, and we find:
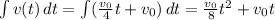
Substituting the limit of integration t = 4, we find:
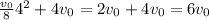
And substituting t = 0, we find 0. So, the result of the integration from 0 to 4 is