Answer:
a) 5 m/s
b) 17.8542 m/s
c) 24.7212 m/s
0.229
Step-by-step explanation:
t = Time taken
u = Initial velocity = 5 m/s
v = Final velocity
s = Displacement
a = Acceleration due to gravity = 9.81 m/s²
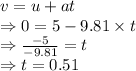
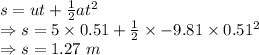
So, the stone would travel 1.27 m up
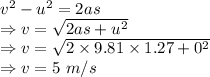
Velocity as the rock passes through the original point is 5 m/s
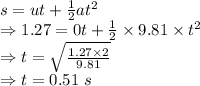
Time taken to reach the original point is 0.51+0.51 = 1.02 seconds
So, total height of the rock would fall is 30+1.27 = 31.27 m
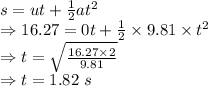
Time taken by the stone to reach 15 m above the ground is 1.82+0.51 = 2.33 seconds

Speed of the ball at 15 m above the ground is 17.8542 m/s
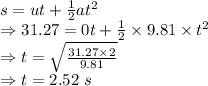
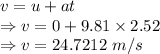
Speed of the stone just before it hits the street is 24.7212 m/s
F = Force
m = Mass = 100 kg
g = Acceleration due to gravity = 9.81 m/s²
s = Displacement = 4 km = 4000 m
P = Power = 1 hp = 745.7 Watt
t = Time taken = 20 minutes = 1200 seconds
μ = Coefficient of sliding friction
F = μ×m×g
⇒F = μ×100×9.81
W = Work done = F×s
P = Work done / Time
⇒P = F×s / t
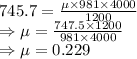
Coefficient of sliding friction is 0.229