Answer:
Probability = 0.58
Explanation:
This problem is solve by using Baye's Probability.
Let P(A) = Probability that operator attended training course = 50% = 0.5
P(B) = Probability that operator not attended training course = 50% = 0.5
Also P(Q) = Probability that operator meet their production quotas
Then, P(Q|A) = 90% = 0.9
P(Q|B) = 65% = 0.65
P(A|Q) = ?
Then by Baye's Theorem,

⇒
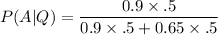
⇒ P(A|Q) = 0.58
which is required probability.