Question

A .5 kg air puck moves to the right at 3 m/s, colliding with a 1.5kg air puck that is moving to the left at 1.5 m/s.

1. Determine the direction and speed of the pucks' motion if they stick to each other after the collision.

2. Suppose instead that the pucks do not stick together. If the 1.5kg puck moves to the right at .231 m/s after the collision, was the collision elastic? Provide evidence!

3. Determine the size and direction of the average force acting on the .5kg puck during the second collision, if the collision lasted for 25 ms.

Answer 1

part (a) v = 1.7 m/s towards right direction

part (b) Not an elastic collision

part (c) F = -228.6 N towards left.

Step-by-step explanation:

Given,

• Mass of the first puck =
  `m_1\ =\ 5\ kg`
• Mass of the second puck =
  `m_2\ =\ 3\ kg`
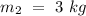
• initial velocity of the first puck =
  `u_1\ =\ 3\ m/s.`
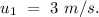
• Initial velocity of the second puck =
  `u_2\ =\ -1.5\ m/s.`

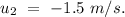
Part (a)

Pucks are stick together after the collision, therefore the final velocities of the pucks are same as v.

From the conservation of linear momentum,

`m_1u_1\ +\ m_2u_2\ =\ (m_1\ +\ m_2)v\\\Rightarrow v\ =\ (m_1u_1\ +\ m_2u_2)/(m_1\ +\ m_2)\\\Rightarrow v\ =\ (5* 3\ -\ 1.5* 1.5)/(5\ +\ 1.5)\\\Rightarrow v\ =\ 1.7\ m/s.`

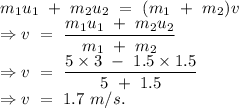
Direction of the velocity is towards right due to positive velocity.

part (b)

Given,

Final velocity of the second puck =
`v_2\ =\ 2.31\ m/s.`

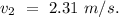
Let
`v_1` be the final velocity of first puck after the collision.

From the conservation of linear momentum,

`m_1u_1\ +\ m_2u_2\ +\ m_1v_1\ +\ m_2v_2\\\Rightarrow v_1\ =\ (m_1u_1\ +\ m_2u_2\ -\ m_2v_2)/(m_1)\\\Rightarrow v_1\ =\ (5* 3\ -\ 1.5* 1.5\ -\ 1.5* 2.31)/(5)\\\Rightarrow v_1\ =\ 1.857\ m/s.`

For elastic collision, the coefficient of restitution should be 1.

From the equation of the restitution,

`v_1\ -\ v_2\ =\ e(u_2\ -\ u_1)\\\Rightarrow e\ =\ (v_1\ -\ v_2)/(u_2\ -\ u_1)\\\Rightarrow e\ =\ (1.857\ -\ 2.31)/(-1.5\ -\ 3)\\\Rightarrow e\ =\ 0.1\\`

Therefore the collision is not elastic collision.

part (c)

Given,

Time of impact = t =
`25* 10^(-3)\ sec`

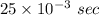
we know that the impulse on an object due to a force is equal to the change in momentum of the object due to the collision,

`\therefore I\ =\ \ m_1v_1\ -\ m_1u_1\\\Rightarrow F* t\ =\ m_1(v_1\ -\ u_1)\\\Rightarrow F\ =\ (m_1(v_1\ -\ u_1))/(t)\\\Rightarrow F\ =\ (5* (1.857\ -\ 3))/(25* 10^(-3))\\\Rightarrow F\ =\ -228.6\ N`

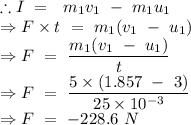
Negative sign indicates that the force is towards in the left side of the movement of the first puck.