Answer:
The Electric field will be 225.92 N/C
Step-by-step explanation:
Given :
- Radius of the hollow sphere R=42.8 cm
- Initial charge on the conducting sphere is

- Magnitude of the point charge
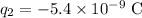
We know that the flux of the electric field through a close surface cab be calculated by using Gauss Law which is

Hence the Electric Field is calculated.
The answer founded out by you seems to be correct and very close to the exact answer and the concept you have used in your answer is also correct.