Question

Combinatorics: what is the coefficient of (a^2)(b^3)(c) in (2a - b + 3c)^6?

Answer 1

The coefficient of a²b³c is -720

Explanation:

Given:
`(2a-b+3c)^6`

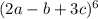
Let 2a-b = x and 3c = y

`(x+y)^6`

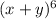
General term of binomial expansion.

• 
  `T_(r+1)=^nC_rx^(n-r)y^r`

where, n=6 , r=1 ( because exponent of c is 1)

`\Rightarrow ^6C_1x^(6-1)y^1`

`\Rightarrow 6(2a-b)^(5)3c`
`\because y=3c, x=2a-b`

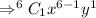
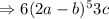
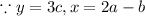
`\Rightarrow 18(2a-b)^(5)c` ----------(1)

Now, we simplify (2a-b)⁵

`T_(r+1)=^5C_r(2a)^(5-r)(-b)^r`

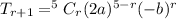
The exponent of b is 3 and a is 2 .

If we take r=3 will get exponent of b is 3 and a is 2

So, put r=3

`T_(4)=^5C_3(2a)^(2)(-b)^3=-40a^2b^3`

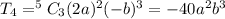
Substitute into equation (1)

`\Rightarrow 18\cdot -40a^2b^3c`

`\Rightarrow -720a^2b^3c`

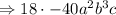
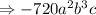
Hence, The coefficient of a²b³c is -720