Answer:
The coefficient of a²b³c is -720
Explanation:
Given:
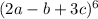
Let 2a-b = x and 3c = y
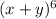
General term of binomial expansion.
where, n=6 , r=1 ( because exponent of c is 1)
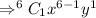
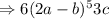
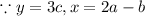
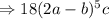 ----------(1)
----------(1)
Now, we simplify (2a-b)⁵
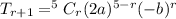
The exponent of b is 3 and a is 2 .
If we take r=3 will get exponent of b is 3 and a is 2
So, put r=3
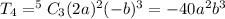
Substitute into equation (1)
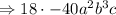
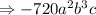
Hence, The coefficient of a²b³c is -720