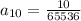Answer:
Explanation:
The first step to solving this problem is verifying if this sequence is an arithmetic sequence or a geometric sequence.
This sequence is arithmetic if:
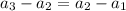
We have that:
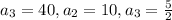
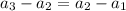
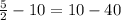
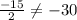
This is not an arithmetic sequence.
This sequence is geometric if:
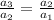
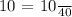
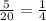
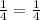
This is a geometric sequence, in which:
The first term is 40, so
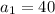
The common ratio is
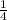 , so
, so
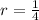 .
.
We have that:
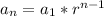
The 10th term is
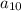 . So:
. So:
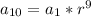
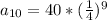
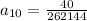
Simplifying by 4, we have: