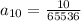Question

In an arithmetic​ sequence, the nth term an is given by the formula an=a1+(n−1)d​, where a1 is the first term and d is the common difference.​ Similarly, in a geometric​ sequence, the nth term is given by 1an=a1•rn−1​, where r is the common ratio. Use these formulas to determine the indicated term in the given sequence.

The 10th term of 40,10, 5/2, 5/8, ....

Answer 1

`a_(10) = (10)/(65536)`

Explanation:

The first step to solving this problem is verifying if this sequence is an arithmetic sequence or a geometric sequence.

This sequence is arithmetic if:

`a_(3) - a_(2) = a_(2) - a_(1)`

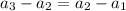
We have that:

`a_(3) = 40, a_(2) = 10, a_(3) = (5)/(2)`

`a_(3) - a_(2) = a_(2) - a_(1)`

`(5)/(2) - 10 = 10 - 40`

`(-15)/(2) \\eq -30`

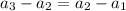
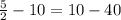
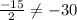
This is not an arithmetic sequence.

This sequence is geometric if:

`(a_(3))/(a_(2)) = (a_(2))/(a_(1))`

`\frac{\frac{5}[2}}{10} = (10)/(40)`

`(5)/(20) = (1)/(4)`

`(1)/(4) = (1)/(4)`

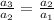
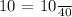
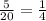
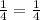
This is a geometric sequence, in which:

The first term is 40, so
`a_(1) = 40`

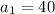
The common ratio is
`(1)/(4)`, so
`r = (1)/(4)`.

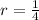We have that:

`a_(n) = a_(1)*r^(n-1)`

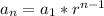
The 10th term is
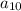`a_(10)`. So:

`a_(10) = a_(1)*r^(9)`

`a_(10) = 40*((1)/(4))^(9)`

`a_(10) = (40)/(262144)`

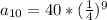
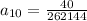
Simplifying by 4, we have:

`a_(10) = (10)/(65536)`