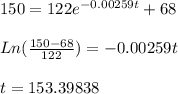Answer:
a.

b.
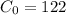
c.

d.
 minutos
minutos
Explanation:
a. Newton's law of cooling states that the speed with which a body is cooled is proportional to the difference between its temperature and that of the medium in which it is found. Then, the initial value problem is given by:
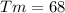

b. The differential equation obtained is a differential equation of separable variables:
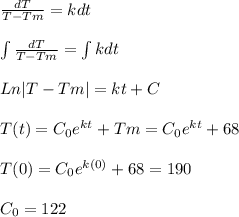
c. After 33 minutes of serving the coffee has cooled to 180°:
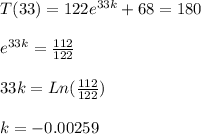
d.