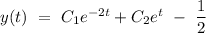Question

Use the variation of parameters method to solve the DE y"+y'- 2y=1

Answer 1

`y(t)\ =\ C_1e^(-2t)+C_2e^t\ -\ (1)/(2)`

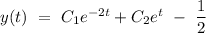
Explanation:

Given differential equation is

y"+y'-2y = 1

`=>\ (D^2\ +\ D\ -\ 2)y\ =\ 1`

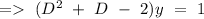
Hence, the characteristics is

`D^2+D-2\ =\ 0`

`=>\ D^2\ +\ 2D\ -\ D\ -2\ =\ 0`

`=> (D+2)(D-1) = 0`

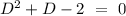
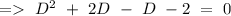
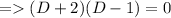
=> D = -2, 1

The general equation of the given differential equation is

`y_c(t)\ =\ C_1e^(-2t)+C_2e^t`

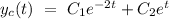
Let's consider that

`y_1(t)\ =\ e^(-2t)`
`y_2(t)\ =\ e^(t)`

`y'_1(t)\ =\ -2e^(-2t)`
`y'_2(t)\ =\ e^t`

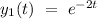
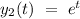
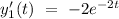
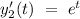
g(t) = 1

Wronskian can be given by,

W = y_1(t)y'_2(t) - y_2(t)y'_1(t)

`=\ e^(-2t).e^t\ -\ e^(t).(-2e^(-2t))`

`=\ e^(-t)\ +\ 2e^(-t)`

`=\ 3e^(-t)`

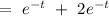
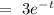
Now, the particular integral can be given by

`y_p(t)\ = \ -y_1(t)\int{(y_2(t).g(t))/(W)dt}\ +\ y_2(t)\int{(y_1(t).g(t))/(W)dt}`

`=\ -e^(-2t)\int{(e^t* 1)/(3e^(-t))dt}\ +\ e^t\int{(e^(-2t)* 1)/(3e^(-t))dt}`

`=\ -e^(-2t)\int{(e^(2t))/(3)dt}\ +\ e^t\int{(e^(-t))/(3)dt}`

`=\ (-e^(-2t))((e^(2t))/(6))\ +\ (e^t)((e^(-t))/(-3))`

`=\ (-1)/(6)\ -\ (1)/(3)`

`=\ (-3)/(6)`

`=\ (-1)/(2)`

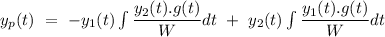
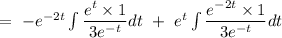
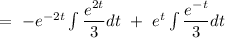
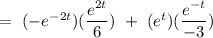
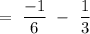
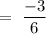
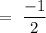
Now,

`y(t)\ =\ y_c(t)\ +\ y_p(t)`

`=\ C_1e^(-2t)+C_2e^t\ -\ (1)/(2)`

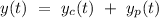
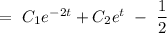
Hence, the complete solution of the given differential equation is

`y(t)\ =\ C_1e^(-2t)+C_2e^t\ -\ (1)/(2)`