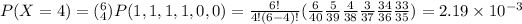Question

3.7.6 .WP A state runs a lottery in which six numbers are randomly selected from 40 without replacement. A player chooses six numbers before the state’s sample is selected. a. What is the probability that the six numbers chosen by a player match all six numbers in the state’s sample? b. What is the probability that five of the six numbers chosen by a player appear in the state’s sample? c. What is the probability that four of the six numbers chosen by a player appear in the state’s sample?

Answer 1

a) 2.60x10^-7

b) 5.31x10^-5

c) 2.19x10^-3

Explanation:

X=number of hits

The probability is the number of desired outcomes divided by the total number of all outcomes.

Then

a) P(X=6)=P({1, 1, 1, 1, 1, 1})=6/40*5/39*4/38*3/37*2/36*1/35=2.60x10^-7

b) P(X=5)=P({0, 1, 1, 1, 1, 1})+P({1, 0, 1, 1, 1, 1})+...+P({1, 1, 1, 1, 1, 0}), every one of these have the same probability

P(X=5)=6P({1, 1, 1, 1, 1, 0})=6*(6/40*5/39*4/38*3/37*2/36*34/35)=5.31x10^-5

c) P(X=4)=P({0, 0, 1, 1, 1, 1})+...+P({1, 1, 1, 1, 0, 0}) every one of these have the same probability.

`P(X=4)=(^6_4)P({1, 1, 1, 1, 0, 0})=(6!)/(4!(6-4)!)((6)/(40) (5)/(39) (4)/(38) (3)/(37) (34)/(36) (33)/(35) )=2.19* 10^(-3)`