Answer:
- Because the mass is also 6 times greater, so the acceleration is the same.
Step-by-step explanation:
Force is mass multiplied by acceleration. This is (in one dimension):
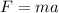
Now, we can see what acceleration will every rock feel:
Lets call
 the force over the first rock, that has a mass
the force over the first rock, that has a mass
 , and lets call
, and lets call
 the force over the second rock, that has a mass
the force over the second rock, that has a mass
 . We can write the following equations:
. We can write the following equations:
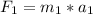
and
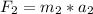 .
.
We also know that:
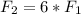 , so:
, so:
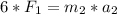 .
.
But the mass is also six times greater.
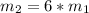
so...
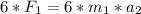 .
.
Now, lets obtain the acceleration. For the first rock we got:
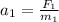
and for the second rock

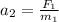
But this is the same acceleration that the first rock has! So, the kinematics will be the same.