Answer:
the electric force between the spheres is maximum when,
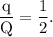
Step-by-step explanation:
Initally, the charge on first sphere = Q.
Now, a portion of q charge is transferred to the second sphere,therefore,
- The charge acquired by the second sphere,
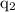 = q.
= q.
- The charge remained on the first sphere,
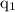 = Q-q.
= Q-q.
Let the two spheres are separated by distance
 .
.
According to the Coulomb's law, the electrostatic force of interaction between the two static point charges
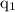 and
and
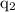 , separated by a distance
, separated by a distance
 is given by
is given by
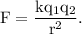
where,
k is the Coulomb's constant.
It is given that both the spheres can be treated as particles and are fixed with a certain separation.
Therefore, the electrostatic force of interaction between the two spheres is given as:
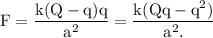
The electrostatic force between the two spheres is extremum for the value of
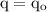 , when
, when
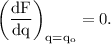
![\rm \left ( (dF)/(dq)\right )_(q=q_o)=\left [ (d)/(dq)\left ((k(Qq-q^2))/(a^2) \right ) \right ]_(q=q_o)\\\\=\left [ (k)/(a^2)(d)/(dq)\left (Qq-q^2 \right ) \right ]_(q=q_o)\\=(k)/(a^2)(Q-2q_o).](https://img.qammunity.org/2020/formulas/physics/high-school/s15nt9lslthuji9k5c8hbaa6rtcgjzt3zt.png)
For,
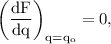
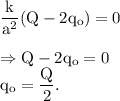
The electrostatic force is maximum when,
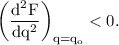
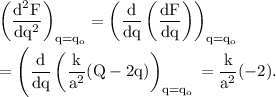
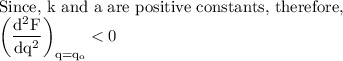
Thus, the electric force between the spheres is maximum when,
