Question

An ideal gas in a cylindrical container of radius r and height h is kept at constant pressure p. The bottom of the container is maintained at temperature T0 while the top at temperature T1. Assuming a linear temperature distribution along the cylinder, calculate the total mass of gas within the container.

Answer 1

`m =(p*(pi)*r^(2)*h*mw)/(R*(T_(1) + T_(O))/(2))`

Step-by-step explanation:

The gas ideal law is

PV= nRT (equation 1)

Where:

P = pressure

R = gas constant

T = temperature

n= moles of substance

V = volume

Working with equation 1 we can get

`n =(PV)/(RT)`

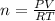
The number of moles is mass (m) / molecular weight (mw). Replacing this value in the equation we get.

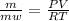`(m)/(mw) =(PV)/(RT)` or

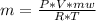`m =(P*V*mw)/(R*T)` (equation 2)

The cylindrical container has a constant pressure p

The volume is the volume of a cylinder this is

`V =(pi)*r^(2)*h`

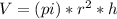
Where:

r = radius

h = height

(pi) = number pi (3.1415)

This cylinder has a radius, r and height, h so the volume is
`V =(pi)*r^(2)*h`

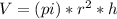
Since the temperatures has linear distribution, we can say that the temperature in the cylinder is the average between the temperature in the top and in the bottom of the cylinder. This is:

`T =(T_(1) + T_(O))/(2)`

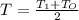
Replacing these values in the equation 2 we get:

`m =(P*V*mw)/(R*T)` (equation 2)

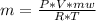`m =(p*(pi)*r^(2)*h*mw)/(R*(T_(1) + T_(O))/(2))`