Question

The plate area is doubled, and the plate separation is reduced to half its initial separation. What is the new charge on the negative plate

Answer 1

Q = 4 Q₀

Step-by-step explanation:

This is an exercise on capacitors, where the capacitance is

C =
`\epsilon_(o) \ (A)/(d)`

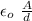
if we apply the given conditions

C = \epsilon_{o} \ \frac{2A}{0.5d}

C = 4 \epsilon_{o} \ \frac{A}{d}

let's call the capacitance Co with the initial values

C₀ = \epsilon_{o} \ \frac{A}{d}

C = 4 C₀

The charge on each plate of a capacitor is

Q = C ΔV

If the potential difference is maintained, the new charge is

Q = 4 C₀ ΔV

let's call

Q₀ = C₀ ΔV

we substitute

Q = 4 Q₀