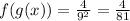Answer:
Listed below
Explanation:
This is a function composition excercise. The idea is to sustitute the value of G(x) in the X's value of the other function.
a)
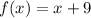 and
and
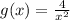
So we replace g(x) on the X of the f(x) function and we get:
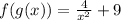
b) We do the same on this excercise:
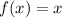 and
and
![g(x)[tex]f(g(x))=(4)/(x+9)](https://img.qammunity.org/2020/formulas/mathematics/high-school/4i965n2vu7ahxt77ki5oukpu8h0gk6akd2.png) [/tex]
[/tex]
We replace and we get:
c) And the same on this one:
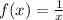 and
and

We replace and we get:
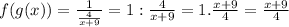
d) Exactly the same on this excercise:
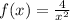 and
and
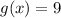
We replace: