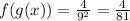Question

Find f(x) and g(x) so that the function can be described as y = f(g(x)).

y = Four divided by x squared. + 9

f(x) = x + 9, g(x) = Four divided by x squared.
f(x) = x, g(x) = Four divided by x. + 9
f(x) = One divided by x., g(x) = Four divided by x. + 9
f(x) = Four divided by x squared., g(x) = 9

Answer 1

im pretty sure its A

Answer 2

Listed below

Explanation:

This is a function composition excercise. The idea is to sustitute the value of G(x) in the X's value of the other function.

a)
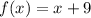`f(x)=x+9` and
`g(x)=(4)/(x^(2) )`

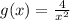
So we replace g(x) on the X of the f(x) function and we get:

`f(g(x))=(4)/(x^(2) ) +9`

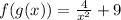
b) We do the same on this excercise:

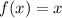`f(x)=x` and
`g(x)[tex]f(g(x))=(4)/(x+9)`[/tex]

We replace and we get:

c) And the same on this one:

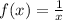`f(x)=(1)/(x)` and
`g(x)=(4)/(x+9)`

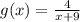
We replace and we get:

`f(g(x))=(1)/((4)/(x+9) ) = 1: (4)/(x+9) =1.(x+9)/(4) =(x+9)/(4)`

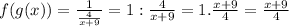
d) Exactly the same on this excercise:

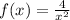`f(x)=(4)/(x^(2) )` and
`g(x)=9`

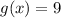
We replace:

`f(g(x))=(4)/(9^(2) ) = (4)/(81)`